| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 12.1 | Exercise 12.2 | Exercise 12.3 |
Chapter 12 Symmetry
Welcome to the solutions guide for Chapter 12, "Symmetry," featured in the latest Class 7 NCERT mathematics textbook for the academic session 2024-25. This chapter revisits and significantly expands upon the beautiful concept of symmetry introduced in Class 6, delving deeper into both reflectional (line) symmetry and introducing the fascinating idea of rotational symmetry. Symmetry is a pervasive concept, visible in nature, art, architecture, and countless mathematical figures, representing balance, harmony, and regularity. These solutions are meticulously designed to provide clear explanations, visual aids (conceptually, as diagrams are crucial in the actual solutions), and step-by-step methods for mastering the exercises in this chapter.
Building upon previous knowledge, the solutions first reinforce the understanding of Line Symmetry (or Reflectional Symmetry). This involves identifying lines about which a figure can be folded so that the two halves match exactly – these are the lines of symmetry. The solutions provide clear illustrations demonstrating these lines for various geometric shapes, letters of the alphabet, and everyday objects. A key focus at the Class 7 level is systematically determining the number of lines of symmetry for various polygons, especially regular polygons. Students will find confirmed counts and visual representations showing, for example:
- An equilateral triangle has 3 lines of symmetry.
- A square has 4 lines of symmetry.
- A regular pentagon has 5 lines of symmetry.
- A circle has infinitely many lines of symmetry passing through its center.
A major advancement in this chapter is the formal introduction and detailed exploration of Rotational Symmetry. A figure exhibits rotational symmetry if it looks exactly the same as its original position after being rotated by a certain angle less than a full turn ($360^\circ$) around a fixed point. The solutions meticulously explain how to:
- Identify the Center of Rotation: The fixed point around which the rotation occurs.
- Determine the Angle of Rotation: The smallest angle (greater than $0^\circ$ and less than or equal to $360^\circ$) through which the figure must be turned to coincide with its original position. Examples include $90^\circ$ for a square, $180^\circ$ for a rectangle, and $120^\circ$ for an equilateral triangle.
- Find the Order of Rotational Symmetry: The number of times the figure matches its original outline during a complete $360^\circ$ rotation. This order is calculated as $360^\circ$ divided by the angle of rotation. For example, a square has order 4 ($360^\circ / 90^\circ = 4$), a rectangle has order 2 ($360^\circ / 180^\circ = 2$), and an equilateral triangle has order 3 ($360^\circ / 120^\circ = 3$). A circle is noted to have infinite order.
Many exercises involve applying these concepts practically. The solutions guide students through completing figures based not only on line symmetry but also on given information about their rotational symmetry (center, angle, or order). This often requires visualizing or sketching the rotation process. The relationship between line symmetry and rotational symmetry is also explored; for instance, figures with multiple lines of symmetry often possess rotational symmetry as well. The solutions help clarify these connections. Diagrams illustrating reflections and rotations are integral to understanding the step-by-step methods provided.
Regarding the rationalized syllabus for 2024-25, Chapter 12, "Symmetry," in the Class 7 NCERT textbook retains its focus on the core concepts of both line symmetry and rotational symmetry (including center, angle, and order). The rationalization process primarily involved adjusting the number and complexity of figures analyzed and construction/completion exercises, ensuring students gain a solid understanding of both symmetry types without excessive intricacy. By engaging with these comprehensive solutions, students can significantly enhance their spatial visualization skills, learn to precisely identify and quantify symmetry properties, and develop a deeper appreciation for the inherent geometric order in shapes and patterns.
Exercise 12.1
Question 1. Copy the figures with punched holes and find the axes of symmetry for the following:

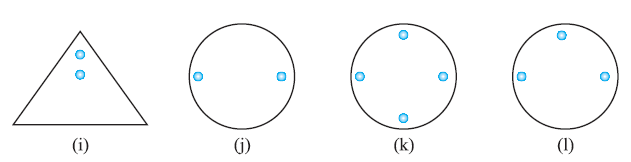
Answer:
Solution:
A figure has a line of symmetry if there is a line about which the figure may be folded so that the two parts of the figure will coincide. For figures with punched holes, the holes must also coincide when folded along the axis of symmetry.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
(j)
(k)
(l)
Question 2. Given the line(s) of symmetry, find the other hole(s):

Answer:
To find the other hole(s) given the line(s) of symmetry, we need to understand the property of symmetry. A figure has a line of symmetry if it can be folded along that line such that the two halves match exactly. If there is a hole on one side of the line, for the figure to be symmetric, there must be a corresponding hole on the other side, which is the reflection of the original hole across the line of symmetry.
(a)
(b)
(c)
(d)
(e)
Question 3. In the following figures, the mirror line (i.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
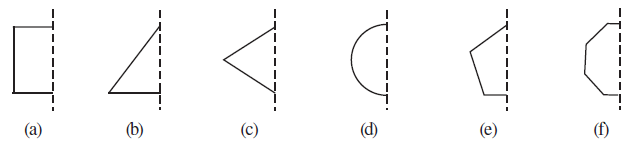
Answer:
To complete each figure given the mirror line (line of symmetry), we need to reflect the given part of the figure across this dotted line. The concept of line of symmetry is closely related to mirror reflection. A shape has line symmetry when one half of it is the mirror image of the other half across the line of symmetry. A mirror line helps visualise this reflection.
While performing mirror reflection, it is important to note the left-right or up-down changes in the orientation of the figure.
(a)
Name of the completed figure is Square.
(b)
Name of the completed figure is Triangle.
(c)
Name of the completed figure is Rhombus.
(d)
Name of the completed figure is Circle.
(e)
Name of the completed figure is Pentagon.
(f)
Name of the completed figure is Octagon.
Question 4. The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry

Identify multiple lines of symmetry, if any, in each of the following figures:
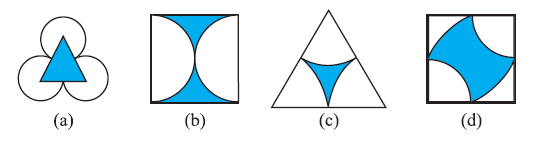
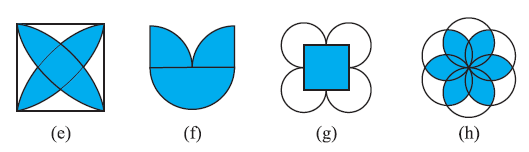
Answer:
We need to identify the lines of symmetry for each of the given figures. A line of symmetry divides a figure into two identical halves that are mirror images of each other. Figures with more than one line of symmetry are said to have multiple lines of symmetry.
(a)
The figure given has 3 lines of symmetry.
So, it has multiple lines of symmetry.
(b)
The figure given has 2 lines of symmetry.
So, it has multiple lines of symmetry.
(c)
The figure given has 3 lines of symmetry.
So, it has multiple lines of symmetry.
(d)
The figure given has 2 lines of symmetry.
So, it has multiple lines of symmetry.
(e)
The figure given has 4 lines of symmetry.
So, it has multiple lines of symmetry.
(f)
The figure given has only 1 line of symmetry.
(g)
The figure given has 4 lines of symmetry.
So, it has multiple lines of symmetry.
(h)
The figure given has 6 lines of symmetry.
So, it has multiple lines of symmetry.
Question 5. Copy the figure given here.
Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?

Answer:
By observing the above figure, Yes, the figure will be symmetrical about both diagonals.
Yes, the figure can be made symmetrical by more than one way.
Question 6. Copy the diagram and complete each shape to be symmetric about the mirror line(s):
Answer:
The concept of line of symmetry is closely related to mirror reflection. A shape has line symmetry when one half of it is the mirror image of the other half. A mirror line, thus helps to visualise a line of symmetry.
While dealing with mirror reflection, care is needed to note down the left-right changes in the orientation.
Reflecting the given part across the dotted line completes the figure as shown below:
(a)
(b)
(c)
Question 7. State the number of lines of symmetry for the following figures:
(a) An equilateral triangle
(b) An isosceles triangle
(c) A scalene triangle
(d) A square
(e) A rectanglecle
(f) A rhombus
(g) A parallelogram
(h) A quadrilateral
(i) A regular hexagon
(j) A circle
Answer:
We need to state the number of lines of symmetry for each of the given geometric figures. A line of symmetry is a line that divides a figure into two identical halves that are mirror images of each other.
(a) An equilateral triangle has three equal sides and three equal angles. It has lines of symmetry passing from each vertex to the midpoint of the opposite side.
Number of lines of symmetry: 3
(b) An isosceles triangle has two equal sides and two equal angles. It has one line of symmetry which passes through the vertex angle and the midpoint of the base (the side opposite the vertex angle).
Number of lines of symmetry: 1
(c) A scalene triangle has all three sides of different lengths and all three angles of different measures. It does not have any line of symmetry.
Number of lines of symmetry: 0
(d) A square has four equal sides and four right angles. It has lines of symmetry passing through the midpoints of opposite sides (2 lines) and along its diagonals (2 lines).
Number of lines of symmetry: 4
(e) A rectangle has opposite sides equal and four right angles. It has lines of symmetry passing through the midpoints of opposite sides. It does not have lines of symmetry along its diagonals unless it is a square.
Number of lines of symmetry: 2
(f) A rhombus has four equal sides and opposite angles equal. It has lines of symmetry along its diagonals. It does not have lines of symmetry passing through the midpoints of opposite sides unless it is a square.
Number of lines of symmetry: 2
(g) A parallelogram has opposite sides parallel and equal, and opposite angles equal. It generally does not have any line of symmetry unless it is a special type of parallelogram like a rhombus, rectangle, or square. For a general parallelogram, there are no lines of symmetry.
Number of lines of symmetry: 0
(h) A quadrilateral is a closed figure with four sides. Without further specification (like square, rectangle, rhombus, kite, etc.), a general quadrilateral does not have any line of symmetry.
Number of lines of symmetry: 0
(i) A regular hexagon has six equal sides and six equal angles. It has lines of symmetry passing through opposite vertices (3 lines) and through the midpoints of opposite sides (3 lines).
Number of lines of symmetry: 6
(j) A circle is a set of points equidistant from a central point. Any line passing through the center of the circle is a line of symmetry (a diameter). Since there are infinitely many diameters, a circle has infinitely many lines of symmetry.
Number of lines of symmetry: Infinitely many
Question 8. What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about.
(a) a vertical mirror
(b) a horizontal mirror
(c) both horizontal and vertical mirrors
Answer:
(a) Letters with symmetry about a vertical mirror (i.e., they appear the same when reflected across a vertical line):
A, H, I, M, O, T, U, V, W, X, Y
(b) Letters with symmetry about a horizontal mirror (i.e., they appear the same when reflected across a horizontal line):
B, C, D, E, H, I, K, O, X
(c) Letters with symmetry about both horizontal and vertical mirrors. These are the letters that appear in both the lists above:
H, I, O, X
Question 9. Give three examples of shapes with no line of symmetry.
Answer:
A shape has no line of symmetry if there is no line across which it can be folded such that the two halves match exactly. Here are three examples of shapes with no line of symmetry:
1. Scalene Triangle: A triangle where all three sides have different lengths and all three angles have different measures.
2. General Parallelogram: A quadrilateral with two pairs of parallel sides, but which is neither a rectangle nor a rhombus (i.e., adjacent sides are not equal, and angles are not $90^\circ$).
3. General Trapezium (Trapezoid): A quadrilateral with at least one pair of parallel sides, where the non-parallel sides are of unequal length (not an isosceles trapezium).
Question 10. What other name can you give to the line of symmetry of
(a) an isosceles triangle?
(b) a circle?
Answer:
We are asked for other names for the line of symmetry of an isosceles triangle and a circle.
(a) For an isosceles triangle, the line of symmetry passes through the vertex angle and the midpoint of the base. This line has several properties and is known by different names depending on which property is highlighted. The line of symmetry is the:
- Angle bisector of the vertex angle.
- Median to the base.
- Altitude to the base.
- Perpendicular bisector of the base.
Any of these terms (specifically referring to the line containing the segment) can be considered another name.
(b) For a circle, any line passing through the center is a line of symmetry. A line segment passing through the center with endpoints on the circle is called a diameter. The line containing this segment is also called a diameter (or the line containing the diameter).
Another name for the line of symmetry of a circle is a Diameter.
Exercise 12.2
Question 1. Which of the following figures have rotational symmetry of order more than 1:

Answer:
Rotational symmetry exists when a figure can be rotated about a central point by an angle less than $360^\circ$ and it looks exactly the same as its original position. The order of rotational symmetry is the number of times the figure coincides with itself during one full rotation ($360^\circ$). We need to find the figures that have rotational symmetry of order more than 1.
(a)
So, the above figure has its rotational symmetry order as 4.
Since $4 > 1$, this figure has rotational symmetry of order more than 1.
(b)
So, the above figure has its rotational symmetry order as 3.
Since $3 > 1$, this figure has rotational symmetry of order more than 1.
(c)
So, the given figure has only one rotational symmetry order, which is 1.
Since $1$ is not more than 1, this figure does not have rotational symmetry of order more than 1.
(d)
So, the above figure has its rotational symmetry order as 2.
Since $2 > 1$, this figure has rotational symmetry of order more than 1.
(e)
So, the above figure has its rotational symmetry order as 3.
Since $3 > 1$, this figure has rotational symmetry of order more than 1.
(f)
So, the above figure has its rotational symmetry order as 4.
Since $4 > 1$, this figure has rotational symmetry of order more than 1.
By observing all the figures (a), (b), (c), (d), (e) and (f) mentioned in the provided solution, those having rotational symmetry of order more than 1 are:
Figures with order $> 1$: (a), (b), (d), (e), (f). Note that figure (c) has order 1. However, the provided solution's concluding sentence lists (a), (b), (c), (d), (e), and (f). Following the final statement from the provided solution:
Figures (a), (b), (c), (d), (e) and (f) have rotational symmetry of order more than 1.
Question 2. Give the order of rotational symmetry for each figure:

Answer:
The order of rotational symmetry of a figure is the number of times the figure looks exactly the same during a full rotation of $360^\circ$ about its center.
(a)
So, the above figure has its rotational symmetry as 2.
(b)
So, the above figure has its rotational symmetry as 2.
(c)
So, the above figure has its rotational symmetry as 3.
(d)
So, the above figure has its rotational symmetry as 4.
(e)
So, the above figure has its rotational symmetry as 4.
(f)
So, the above figure has its rotational symmetry as 5.
(g)
So, the above figure has its rotational symmetry as 6.
(h)
So, the above figure has its rotational symmetry as 3.
Exercise 12.3
Question 1. Name any two figures that have both line symmetry and rotational symmetry.
Answer:
We need to identify two geometric figures that possess both line symmetry and rotational symmetry of order greater than 1.
A figure has line symmetry if it can be divided into two identical mirror-image halves by a line.
A figure has rotational symmetry of order greater than 1 if it coincides with itself after being rotated by an angle less than $360^\circ$ about its center.
Here are two examples of such figures:
1. Square:
- A square has 4 lines of symmetry (two through midpoints of opposite sides and two along the diagonals).
- A square has rotational symmetry of order 4 (it looks the same after rotations of $90^\circ, 180^\circ,$ and $270^\circ$).
2. Circle:
- A circle has infinitely many lines of symmetry (any line passing through its center).
- A circle has rotational symmetry of infinite order (it looks the same after rotation by any angle about its center).
Other examples include an Equilateral Triangle (3 lines of symmetry, order 3 rotational symmetry) and a Regular Hexagon (6 lines of symmetry, order 6 rotational symmetry).
Question 2. Draw, wherever possible, a rough sketch of
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
Answer:
We will provide descriptions and sketch ideas for each type of figure based on the given symmetry properties.
(i) A triangle with both line and rotational symmetries of order more than 1.
A triangle having rotational symmetry of order more than 1 must be an equilateral triangle. An equilateral triangle has rotational symmetry of order 3 (it looks the same after rotations of $120^\circ, 240^\circ,$ and $360^\circ$). An equilateral triangle also has 3 lines of symmetry (lines joining each vertex to the midpoint of the opposite side).
Sketch description: Draw a triangle with all three sides of equal length.
(ii) A triangle with only line symmetry and no rotational symmetry of order more than 1.
A triangle with only line symmetry and no rotational symmetry of order greater than 1 is an isosceles triangle which is not equilateral. An isosceles triangle has exactly one line of symmetry (passing through the vertex angle and the midpoint of the base). Its rotational symmetry is only of order 1 (only coincides after a $360^\circ$ rotation).
Sketch description: Draw a triangle with two sides of equal length and the third side of a different length.
(iii) A quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
A quadrilateral with rotational symmetry of order more than 1 but no line symmetry is a parallelogram that is not a rhombus, rectangle, or square. A parallelogram has rotational symmetry of order 2 about the intersection of its diagonals. However, it does not have any line of symmetry unless it is one of the special types mentioned.
Sketch description: Draw a quadrilateral with two pairs of parallel sides, where adjacent sides are not equal in length and angles are not right angles.
(iv) A quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
A quadrilateral with line symmetry but only rotational symmetry of order 1 can be an isosceles trapezium or a kite (that is not a rhombus).
Sketch description (Isosceles Trapezium): Draw a quadrilateral with exactly one pair of parallel sides, and the non-parallel sides are equal in length. It has one line of symmetry joining the midpoints of the parallel sides.
Sketch description (Kite - not a rhombus): Draw a quadrilateral with two pairs of equal-length adjacent sides, where the adjacent pairs are not equal (i.e., two short sides adjacent, two long sides adjacent). It has one line of symmetry along the diagonal connecting the vertices where the unequal side pairs meet.
Question 3. If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Answer:
Let's consider figures with two or more lines of symmetry.
A figure with two or more lines of symmetry generally implies a certain level of regularity or balance around its center. If a figure has two distinct lines of symmetry intersecting at a point, reflection across the first line followed by reflection across the second line is equivalent to a rotation about the intersection point by an angle equal to twice the angle between the lines.
For example:
- A rectangle has 2 lines of symmetry (horizontal and vertical through the center). It has rotational symmetry of order 2 (rotation by $180^\circ$).
- A rhombus has 2 lines of symmetry (along the diagonals). It has rotational symmetry of order 2 (rotation by $180^\circ$).
- A square has 4 lines of symmetry. It has rotational symmetry of order 4.
- An equilateral triangle has 3 lines of symmetry. It has rotational symmetry of order 3.
In all these cases, figures with two or more lines of symmetry do have rotational symmetry of order more than 1. It is a geometric property that having multiple lines of reflection implies rotational symmetry.
So, the answer is Yes. If a figure has two or more lines of symmetry, it must have rotational symmetry of order more than 1.
Question 4. Fill in the blanks:
| Shape | Centre Of Rotation | Order Of Rotation | Angle Of Rotaion |
|---|---|---|---|
| Square | |||
| Rectangle | |||
| Rhombus | |||
| Equilateral Triangle | |||
| Regular Hexagon | |||
| Circle | |||
| Semi - Circle |
Answer:
We need to fill in the table with the correct information about the rotational symmetry of each given shape.
The Centre of Rotation is the point about which the figure is rotated.
The Order of Rotation is the number of times the figure looks exactly the same during a $360^\circ$ rotation (excluding the $360^\circ$ position which is always a coincidence).
The Angle of Rotation is the smallest angle by which the figure can be rotated to coincide with its original position. It is given by $\frac{360^\circ}{\text{Order of Rotation}}$.
Here is the completed table:
| Shape | Centre Of Rotation | Order Of Rotation | Angle Of Rotation |
| Square | Intersection of diagonals | 4 | $90^\circ$ |
| Rectangle | Intersection of diagonals | 2 | $180^\circ$ |
| Rhombus | Intersection of diagonals | 2 | $180^\circ$ |
| Equilateral Triangle | Centroid | 3 | $120^\circ$ |
| Regular Hexagon | Centre | 6 | $60^\circ$ |
| Circle | Centre | Infinitely many | Any angle |
| Semi - Circle | Midpoint of diameter | 1 | $360^\circ$ |
Question 5. Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
Answer:
We need to identify quadrilaterals that have at least one line of symmetry and rotational symmetry of order greater than 1 (meaning it looks the same after a rotation of less than $360^\circ$).
Let's consider the common quadrilaterals:
1. Square: Has 4 lines of symmetry and rotational symmetry of order 4 ($90^\circ$). Both conditions are met.
2. Rectangle (not a square): Has 2 lines of symmetry and rotational symmetry of order 2 ($180^\circ$). Both conditions are met.
3. Rhombus (not a square): Has 2 lines of symmetry (its diagonals) and rotational symmetry of order 2 ($180^\circ$). Both conditions are met.
4. Parallelogram (not a rhombus or rectangle): Has no line symmetry but has rotational symmetry of order 2. It doesn't meet the line symmetry condition.
5. Kite (not a rhombus): Has 1 line of symmetry but rotational symmetry of order 1. It doesn't meet the rotational symmetry order > 1 condition.
6. Isosceles Trapezium: Has 1 line of symmetry but rotational symmetry of order 1. It doesn't meet the rotational symmetry order > 1 condition.
The quadrilaterals that have both line and rotational symmetry of order more than 1 are:
Square, Rectangle, and Rhombus.
Question 6. After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Answer:
If a figure looks exactly the same as its original position after a rotation by $60^\circ$ about a center, this means that $60^\circ$ is an angle of rotational symmetry.
If a figure has rotational symmetry by an angle $x$, then it will also have rotational symmetry by any multiple of $x$. That is, the figure will look the same after rotations of $k \times x$, where $k$ is a positive integer.
In this case, the given angle of rotation is $60^\circ$. So, the figure will look the same after rotations by multiples of $60^\circ$. We consider rotations within a full circle ($360^\circ$).
The angles are:
- $1 \times 60^\circ = 60^\circ$ (This is the given angle)
- $2 \times 60^\circ = 120^\circ$
- $3 \times 60^\circ = 180^\circ$
- $4 \times 60^\circ = 240^\circ$
- $5 \times 60^\circ = 300^\circ$
- $6 \times 60^\circ = 360^\circ$ (A rotation by $360^\circ$ always brings any figure back to its original position)
The question asks for the other angles besides $60^\circ$ at which this will happen. These are the angles from the list above, excluding $60^\circ$ and typically excluding $360^\circ$ as it's always a coincidence.
The other angles are $\mathbf{120^\circ}$, $\mathbf{180^\circ}$, $\mathbf{240^\circ}$, and $\mathbf{300^\circ}$.
Question 7. Can we have a rotational symmetry of order more than 1 whose angle of rotation is
(i) 45°?
(ii) 17°?
Answer:
A figure has rotational symmetry of order $n$ if it coincides with itself $n$ times during a full rotation of $360^\circ$ about its center. The angle of rotation for such symmetry is given by $\alpha = \frac{360^\circ}{n}$.
For the order of rotational symmetry to be more than 1 ($n > 1$), the angle of rotation $\alpha$ must be a divisor of $360^\circ$, such that $\frac{360^\circ}{\alpha}$ is an integer greater than 1.
(i) Angle of rotation is $45^\circ$.
We check if $\frac{360^\circ}{45^\circ}$ is an integer greater than 1.
Order $= \frac{360^\circ}{45^\circ} = 8$
Since 8 is an integer and $8 > 1$, a figure can have rotational symmetry of order 8 with an angle of rotation of $45^\circ$. An example is a regular octagon.
So, Yes, we can have rotational symmetry of order more than 1 whose angle of rotation is $45^\circ$.
(ii) Angle of rotation is $17^\circ$.
We check if $\frac{360^\circ}{17^\circ}$ is an integer greater than 1.
Order $= \frac{360^\circ}{17^\circ}$
Since $360$ is not perfectly divisible by $17$ (17 is a prime number and 360 is not a multiple of 17), $\frac{360}{17}$ is not an integer.
For the order of rotational symmetry to be a positive integer $n > 1$, the angle of rotation must be an integral divisor of $360^\circ$. Since $17^\circ$ is not an integral divisor of $360^\circ$, it cannot be the angle of rotation for a rotational symmetry of order greater than 1 for a finite figure.
So, No, we cannot have rotational symmetry of order more than 1 whose angle of rotation is $17^\circ$.

